ကိုဗစ်ရောဂါပြန့်ပွားမှုနှင့် ဂဏန်းမသင် လာဘ်မမြင်

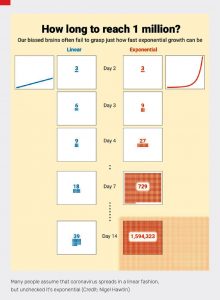
အချိန်နှင့်အမျှ အဆတိုးခြင်း

သင်္ချာပညာတွင် Exponential Growth (အဆတိုးကြီးထွားခြင်း) ဆိုတာရှိသည်။ မိတ်ဆွေ သင်္ချာပါမောက္ခကတော့ Exponential Growth ကို အထပ်လိုက် အဆတိုး ကြီးထွားမှုဟု ပြန်ဆိုချင်သတဲ့။ ကျနော်ကတော့ ကိုယ်လိုသူလို လူပြိန်းနားလည်အောင် အချိန်နှင့်အမျှအဆတိုးခြင်းဟု ပြန်ဆိုလိုက်ပါသည်။ “ကြီးထွား”ဆိုတာကို ဖြုတ်ပစ်ပြီး “အချိန်နှင့်အမျှ” ဆိုတာ ဖြည့်စွက်ပါသည်။ ကျနော်တင်ပြမည့် အကြောင်းအရာနှင့် လိုက်လျောညီထွေဖြစ်အောင် မွမ်းမံလိုက်ခြင်းပါပဲ။

သူ့အကြောင်းရှင်းမပြခင် Exponential Growth (အစဉ်အတိုင်းတိုးခြင်း၊ အဖြောင့် တိုးခြင်း)ကို ရှေးဦးစွာ ရှင်းပြချင်ပါသည်။ ဒါက နားလည်ရလွယ်သည်။ ဥပမာ-ခင်ဗျားခြံထဲမှအပင်က တရက်ကို ပန်းသီးသုံးလုံးသီးတယ် ဆိုပါစို့။ နှစ်ရက်မှာ ပန်းသီး ခြောက်လုံး၊ သုံးရက်မှာ ပန်းသီးကိုးလုံး ရမည်။ Exponential Growth ကျတော့ အချိန် ရလာသည်နှင့်အမျှ တိုးပွားမှုနှုန်းက အရှိန်တက်လာသည်။ အချိန်ကြာလေ၊ တိုးပွားမှု ပမာဏ ကြီးလာလေ။ လူဦးရေတိုးနှုန်းက Exponential Growth အတိုင်းသွားတာ။ မွေးနှုန်းတက်လာလေလေ၊ လူဦးရေတိုးနှုန်းမြန်လာလေလေ။ တဖက်စာမျက်နှာမှပုံကို ကြည့်ပါက တိုးပွားမှုနှစ်ခုကြား ပမာဏက အချိန်နှင့်အမျှ မည်ရွေ့မည်မျှ ကွာဟသွား သည်ကို ရှင်းလင်းစွာ မြင်နိုင်ပါသည်။

 

စစ်တုရင်ပေါ်က ဂျုံစေ့

အချိန်နှင့်အမျှအဆတိုးခြင်း ဆိုတာကို လူအများစုက သတိမမူမိသော်လည်း သင်္ချာပညာရှင်တွေက ဟိုးရှေးရှေးကတည်းက သိခဲ့ကြတာ။ လူသိအများဆုံး ပုံပြင် တခုက စစ်တုရင်စထွင်ခဲ့သည့် ဗြဟ္မဏပညာရှိ ဆစ်ဆာအိဘင်ဒါဟီးရ် (Sissa ibn Dahir) နှင့် ပတ်သက်နေသည်။ ဒီကစားနည်းကို တီထွင်ခဲ့သည့် ပညာရှိကြီးကို ဘုရင် ကြီးက ဆုတော်လာဘ်တော်ချီးမြှင့်လို၍ သူလိုရာ ဆုတောင်းခွင့်ပြုသည်။ ပညာရှိကြီး က စစ်တုရင်ကွက် ၆၄ ကွက်ထဲက ပထမအကွက်ထဲ ဂျုံတစေ့ထည့်ပေးပါ။ ဒုတိယ အကွက်ထဲ ဂျုံနှစ်စေ့ထည့်ပေးပါ။ တတိယအကွက်ထဲ ဂျုံလေးစေ့ထည့်ပေးပါ စသည် ဖြင့် တကွက်တိုးတိုင်း ဂျုံစေ့နှစ်ဆ တိုးတောင်းသွားသည်။ ဂျုံစေ့လေးတွေကို ဒီအတိုင်း ၆၄ ကွက်ပြည့်အောင် ထည့်ပေးပါ။ သူလိုချင်တဲ့ဆုတော်က ဒါပါပဲဟု ပညာရှိက ဘုရင်ကြီးကို လျှောက်တင်သည်။

ဘုရင်ကြီးက သူ့ပညာရှိကြီး၏ နှိမ့်ချမှုကို ရယ်သွမ်းသွေးတော်မူသည်။ “ဆရာ တောင်းဆိုတာ နည်းလှချည်ကလား”ပေါ့။ တကယ် တွက်ကြည့်လိုက်တဲ့အခါကျမှ ဘုရင်ကြီး မျက်လုံးပြူးသွားသည်။ ပညာရှိကြီးတောင်းတဲ့ ဂျုံစေ့ အရေအတွက်က မတန်တဆများနေတာ တွေ့ရသည်။ သူတောင်းဆို တဲ့ ဂျုံစေ့အရေအတွက်က ဘုရင်ကြီး၏ နိုင်ငံတော်တဝန်းက ရနိုင်တဲ့ ဂျုံပမာဏထက် အဆမတန် သာလွန်များပြားနေကြောင်း ဘဏ္ဍာတော်ထိန်းတွေက ဘုရင်ကြီးကို သံတော်ဦးတင်သည်။ တွက်ချက်လို့ရတဲ့ဂျုံစေ့က စုစုပေါင်း (၁၈,၄၄၆,၇၄၄,၀၇၃,၇၀၉,၅၅၁,၆၁၅) ရှိသည်တဲ့။ ၁၈ ကွင်တီ လီယံကျော်ကျော်။ (၁ ကွင်တီလီယံ = ၁ ဂဏန်းနောက် သုည ၁၈ လုံး) ယနေ့ခေတ် ကမ္ဘာ တဝန်းလုံး   နှစ်စဉ်ထွက်ရှိသော ဂျုံပမာဏထက် အဆ ၂၀ဝ၀ ခန့် ရှိသည်တဲ့။

နောက်ဆုံး ရယ်သွမ်းသွေးသူက ဗြဟ္မဏ ပညာရှိကြီး ဖြစ်မည်။

 

ပြန်သုံးဆယ် ဆန်ကိုစားတယ်၊ မှားချက်ကနာ

အချိန်နှင့်အမျှ အဆတိုးခြင်းဆိုတာကို ရေရေရာရာ မသိ၍ ကင်းဝန်မင်းကြီး ဦးကောင်း တယောက် မင်းတုန်းမင်းကြီး၏ ရယ်သွမ်းသွေးခံရ ပုံအကြောင်း ဆရာကြီး(ဦး)လေးမြိုင်က “အစား မှားသော     ကင်းဝန်” ဆောင်းပါးနှင့် မှတ်တမ်းတင် သည်။ (လောကကြေးမုံ၊ ၁၉၉၈)

ကင်းဝန်မင်းကြီး အသက် သုံးဆယ်ကျော် အရွယ် ရာထူးဘွဲ့ထူးမကြီးမြင့်သေးမီကာလ တနေ့ တွင် မမေ့နိုင်သောဖြစ်ရပ်တခုကို ကြုံခဲ့ရဖူးသည်။ စကားတခွန်းကြောင့် ပေါ်ပေါက်လာသော အမှတ် ရဖွယ် ဖြစ်ရပ်ပေတည်း။

ထိုစဉ်က မောင်ကောင်းအပါအဝင် အကြီး တော် ဘဏ္ဍာစာရေးများ ကွမ်းရေတော်၊ ထီးတော် မိုး စသူတို့ မင်းတုန်းမင်း၏အနီးတွင် ရှိနေကြ၏။

“ဟေ့၊ မင်းတို့အထဲမှာ ဆန်တစေ့ကစပြီး အပြန်သုံးဆယ်အထိ ကုန်အောင်စားနိုင် တဲ့သူ ရှိသလား၊ စားနိုင်သူကို မြင်းတစီးနဲ့ ပုဆိုးတထည်ဆုချမယ်ကွဲ့၊ အေး ကုန်အောင် မစားနိုင်ရင်တော့ ဥယျာဉ်တော်မှာ ရေလောင်းရလိမ့်မယ်၊ ကဲ ဘယ်သူစွမ်းသလဲ၊ စား ကြည့်ကြပေတော့ဂ

မင်းတုန်းမင်းသည် ပျော်ရွှင်ရယ်မောလိုသဖြင့် အမှုထမ်းများကို အကဲစမ်း ပြော ကြားလိုက်ခြင်းဖြစ်၏။

“ကျွန်တော်မျိုး စားနိုင်ကြောင်းပါဘုရား”

မောင်ကောင်းနှင့် အခြား ဘဏ္ဍာစာရေးဦးမိုးတို့ ပြိုင်တူပြောကြားလိုက်ခြင်း ဖြစ်သည်။

“အိမ်း သည်လိုဆိုရင် ဘဏ္ဍာစိုးများက ဆန်ထုတ်ပေးကြပေတော့၊ ဆန်မထုတ်မီ ဆန်ဘယ်မျှလောက်ထုတ်ရမယ် တွက်ချက်ကြည့်ကြအုံး ကွယ်ရို့”

မင်းတုန်းမင်းက ခပ်ရွှင်ရွှင်ခပ်ပြုံးပြုံးဖြင့် မိန့်ကြားလိုက်သဖြင့် ဘဏ္ဍာစာရေးများ နှင့်ဘဏ္ဍာစိုးများ စားရမည့်ဆန်အရေအတွက်ကို စာရင်းပြုကြရသည်။

ဆန်တစေ့မှ နှစ်စေ့၊ နှစ်စေ့မှ လေးစေ့၊ လေးစေ့မှ ရှစ်စေ့၊ ရှစ်စေ့မှ ၁၆ စေ့၊ ၁၆ စေ့မှ ၃၂ စေ့၊ ၃၂ စေ့မှ ၆၄ စေ့ စသည်ဖြင့် တပြန်တစ်ဆ တိုး၍တိုး၍ရေတွက်ကြရာ အကြိမ် ၃၀ ရှိသောအခါ ဆန်စေ့ပေါင်း ၁၀၇ ကုဋေ ကျော်လာသည်ကို တွေ့ကြရလေ၏။

ယင်းကို တင်းဖွဲ့လိုက်သောအခါ ဆန်တင်းပေါင်း ၁,၃၀၀ ကျော်ဖြစ်လာ၏။(ဆန် တတင်းမှာ ဆန်စေ့ပေါင်း ၇၆၄,၀၀၀ ရှိသည်ဟူသော မြန်မာ့ရိုးရာသင်္ကေတ သင်္ချာ နည်းဖြင့် တွက်ယူကြခြင်းဖြစ်၏။)

ဘဏ္ဍာစိုး၊ ဘဏ္ဍာစာရေးစသူတို့သည် တအံ့တဩဖြစ်ကြရသည်။ မောင်ကောင်း နှင့် ဘဏ္ဍာစာရေးဦးမိုးတို့မှာ အံ့ဩရုံမက မျက်စိမျက်နှာပျက်လျက် ရှိနေကြ၏။ မင်းတုန်းမင်းကား သဘောတွေ့ကာ ပြုံးရွှင်၍နေလေသည်။

“ကျွန်တော်မျိုး စားနိုင်ကြောင်းပါဘုရား” ဟု အဆိုပြုသူနှစ်ဦးတို့ ဆန်တင်းပေါင်း တထောင့်သုံးရာကျော်ကို မည်သို့ ကုန်အောင်စားကြမည်နည်း။ လူတယောက်အဖို့ နှစ်ပေါင်း ၆၀ဝ ခန့် စားယူရမည့် ဆန်များပေတည်း။

သို့သော်လည်း ကင်းဝန်လောင်းလျာ မောင်ကောင်း၏ လက်တန်းကဗျာကြောင့် မင်းတုန်းမင်းကြီးက သူ့ကို ဥယျာဉ်တော် ရေလောင်းရသည့်ဒဏ်မှ ကင်းလွတ်ခွင့်ပေး လိုက်သည်။ သင်္ချာသဘောတရားသာ မသိတာ၊ စာဆိုရာမှာတော့ မောင်ကောင်းက စွမ်းသည်။ သူ့လက်တန်းကဗျာက ဤသို့။

 

ပုဆိုးနှင့်မြင်းပါ

ဆုတော်ခံမယ်လို့

ပြန်သုံးဆယ် ဆန်ကိုစားတယ်

မှားချက်ကနာ။

 

နောက်တစ်ခါ

ကြောက်ပါပေါ့ သက်ဆုံး

သည်တစ်ပွဲမှာဖြင့် အလွဲကံချော်လို့

ဥယျာဉ်တော် ရေကိုလောင်းရတယ်

ငယ်ပေါင်း ယဉ်ဟန်ကြွယ်တဲ့

ဆင်ကြန်မယ် ဖြူပြာနွဲ့ရယ်

မင်း ကူလှည့်ဦး။

 

မင်းတုန်းမင်းက ခေတ်မီသည်။ အချိန်နှင့်အမျှ အဆတိုးခြင်းသဘောကိုသိသည်။

 

သိသလိုလိုနှင့် မသိသူများ

အချိန်နှင့်အမျှ အဆတိုးခြင်းသဘောက နားလည်ရလွယ်သည်ဟု ထင်ရသော်လည်း ယနေ့ခေတ်မှာပင် လက်တွေ့ကျကျသိသူ သိပ်မရှိလှဟုဆိုသည်။ တက္ကသိုလ် ဘွဲ့ရများပင်လျှင် ဤသဘောတရားကို ပိုင်ပိုင်နိုင်နိုင်မသိဟု စစ်တမ်းတခုကဆိုသည်။ ပညာတတ်အများစုက တခုခုကို ဆုံးဖြတ်ချက်ချရာမှာ တွေးတွေးဆဆလုပ်ပြီးမှ ချသည်ထက် သူတို့စိတ်ထဲ ရုတ်ချည်းပေါ်လာသည့်ဆုံးဖြတ်ချက် (Intuition) ကို ဦးစား ပေးကြသည်က များသည်။ အထူးသဖြင့် အချိန်နှင့်အမျှ အဆတိုးခြင်းသဘောကို သိသည်ဟု သူတို့ဘာသာထင်သော်လည်း လက်တွေ့ဘဝ၌ ကျင့်သုံးလေ့မရှိဟုဆို သည်။ ပိုဆိုးတာက သူတို့မသိမှန်း သူတို့ကိုယ်နှိုက်က မသိခြင်း (bias blind spot) ပါပဲ။

ကိုဗစ်ကပ်ရောဂါအစ ၂၀၂၀ နှစ်ဦးပိုင်းကာလတွင် သုတေသီများက ဤအချိန်နှင့် အမျှ အဆတိုးခြင်းသဘောကို လူများစု မသိနားမလည်ခြင်းနှင့် လူထုအတွင်း ကိုဗစ် ရောဂါ ကူးစက်ပြန့်ပွားခြင်း- ယင်းတို့နှစ်ခုကြား ဆက်စပ်မှုရှိမရှိ ဆန်းစစ်လာကြသည်။ ကိုဗစ်ရောဂါကူးစက်ပြန့်နှံ့ပုံက ဘယ်လမ်းကြောင်းအတိုင်း သွားသလဲ။ ရောဂါကူးစက် ပြန့်ပွားပုံဖြစ်စဉ်ကိုစောင့်ကြည့်လေ့လာသူများက ကိုဗစ်ရောဂါကို ထိန်းချုပ်မှုမလုပ်ဘဲ လွှတ်ပေးထားလိုက်ပါက သုံးရက်-လေးရက်အတွင်း ကိုဗစ်ရောဂါကူးစက်ခံရသည့် လူနာ နှစ်ဆတက်သွားမည်ဟုဆိုသည်။ ကူးစက်နှုန်းက အချိန်နှင့်အမျှ အဆတိုးခြင်း လမ်းကြောင်းအတိုင်းသွားတာ တွေ့ရသည်။

မတ်လမှာ ဂျာမန်တက္ကသိုလ်နှစ်ခုမှ ပညာရှင်သုံးဦး ပူးပေါင်းပြီး ကိုဗစ်ရောဂါ ကူးစက်ပြန့်ပွားနိုင်ခြေနှင့်ပတ်သက်သည့် ပြည်သူလူထု၏အမြင်/သဘောထားကို အွန်လိုင်းမှ စစ်တမ်းကောက်သည်။ ကိုဗစ်ရောဂါဆိုတာ အချိန်နှင့်အမျှ အဆတိုးပျံ့နှံ့ နိုင်တယ်ဆိုတာ အများစုသော ပြည်သူလူထုကြီးအနေနှင့် လုံးဝသတိမမူကြောင်း စစ်တမ်းထွက်လာသည်။ ဒီလိုသတိမမူမိတော့ အကျိုးဆက်က ဘာဖြစ်မလဲ။ အကျိုးဆက် အနေနှင့် လူများစုက ရောဂါတိုးနှုန်းကို လျှော့တွက်ကြသည်။ ဒီအမြင် ဒီအတွေးတွေက ရောဂါကို ဘယ်လို တားဆီးကာကွယ်မလဲဆိုတဲ့ လုပ်ရပ်တွေ၊ အပြုအမူတွေနှင့်   တိုက်ရိုက် ဆက်နွှယ်နေပြန်သည်။ အချိန်နှင့်အမျှအဆတိုးခြင်း သဘောတရားကို မသိ လေလေ၊ ရောဂါကူးစက်နိုင်ခြေနှင့် ရောဂါတိုးနှုန်းကို လျှော့တွက်လေလေ။ ရောဂါ ကူးစက်နိုင်ခြေနှင့် ရောဂါတိုးနှုန်းကို လျှော့တွက်လေလေ၊ လူချင်းခပ်ခွာခွာနေဖို့၊ နှာခေါင်းစည်းသုံးဖို့၊ လက်ဆေးဖို့စတဲ့ ကျန်းမာရေးဌာနက òန်ကြားထားတဲ့ ရောဂါ ကာကွယ်ရေး လုပ်ငန်းတွေကို မလိုက်နာလေလေဆိုတာ သုတေသီတွေ သွားတွေ့ သည်။ အိန္ဒိယနိုင်ငံ ဘန်ဂလိုမှ ပညာရှင်နှစ်ဦးနှင့် အမေရိကန် အိုင်အိုဝါပြည်နယ် တက္ကသိုလ်မှ ပညာရှင်တဦး၏ လူထုအခြေပြုစစ်တမ်းများကလည်း ဂျာမန်ပညာရှင်တို့၏ သုတေသနတွေ့ရှိချက်ကို ထောက်ခံအတည်ပြုသည်။

 

ပညာရှင်များ၏အကြံပြုချက်

ရောဂါဖြစ်ပွားမှုနှုန်းနှင့်ပတ်သက်၍ မီဒီယာအများစုက လက်ရှိ ဖော်ပြသုံးစွဲနေ သော လော့ဂရစ်သမ်စကေး (Logarithmic Scale) က အချိန်နှင့်အမျှ ရောဂါ အဆ တိုးခြင်းကို ဖော်ပြနိုင်စွမ်းမရှိဟု ပညာရှင်များက သဘောရသည်။ လူနာဦးရေကို ရိုးရိုး ဇယား (Table) နှင့်ဖော်ပြသည်ကမှ Logarithmic Scale နှင့်ဖော်ပြသည်ထက် ပို၍သင့်တော်ကြောင်း သူတို့ကပြောသည်။

ဂျာမန်တက္ကသိုလ် သုတေသီများက သူတို့ စစ်တမ်းကောက်သည့်သူတွေကို အချိန်နှင့်အမျှ အဆတိုးခြင်းသဘောကို သူတို့တတွေ အမှတ်ရအောင် ပြန်ပြောပြသည်။ ပြီးတော့ သူတို့ကို ရောဂါ ပြန့်ပွားနှုန်း၊ ရောဂါတိုးနှုန်း တွက်ချက်ခိုင်းသည်။ ရောဂါတိုးနှုန်းနှင့်ပတ်သက်၍ သူတို့၏ ခန့်မှန်းနိုင်စွမ်း၊ တွက်ဆနိုင်စွမ်း သိသိသာသာကြီး မြင့်တက် လာတာ တွေ့ရသည်။ တဖက်ကလည်း ရောဂါကာကွယ်ရေးလုပ်ငန်းများ (လူချင်း ခပ်ခွာခွာနေခြင်း စသည်တို့)အပေါ် သူတို့၏အမြင်၊ သဘောထားများ အကောင်းဘက် ပြောင်းလဲလာတာ တွေ့ရသည်။ ထို့အပြင် ရောဂါကူးစက်ခံရသူဦးရေကို ဖော်ပြရုံ သက်သက်ထက် ဒီရောဂါက အချိန်တိုတိုအတွင်း လူပေါင်းမည်မျှကို ကူးစက်သွားပုံ၊ လူချင်း ခပ်ခွာ ခွာနေခြင်းက ဒီအချိန်တိုတိုလေးကို အချိန်ရှည် ရှည်ကြီးဖြစ်သွားစေပုံ စသည်တို့ကို ဦးစားပေး တင်ပြခြင်းက ပြည်သူလူထုကို ပညာပေးရာ၌ ပို၍ ထိရောက်ကြောင်း ပညာရှင်များကယူဆကြသည်။ ပြဿနာကို ဘယ်လိုပုံဖော်မလဲ၊ ဘယ်ရှုထောင့် ကနေ တင်ပြမလဲ (Framing the issues; Framing the problems) က အရေးကြီးသည်။ ဒီလို ပြော တတ်၊ ပြတတ်မှ လူထုရင်ထဲ ရောက်မည်။ လူထု ရင်ထဲရောက်မှ လူထုရင်ထဲစွဲမည်။ သို့မှသာ အချိန် နှင့်အမျှ ရောဂါအရှိန် တက်သွားတတ်ကြောင်း ပြည်သူလူထု သတိမူမိလာမည်။

အစိုးရနှင့်မီဒီယာက ကိုဗစ်ကပ်ရောဂါအကြောင်း ပြည်သူလူထုကို အသိပေးတင်ပြရာမှာ အချိန်နှင့်အမျှ ရောဂါအဆတိုးခြင်းသဘောတရားကို မကြာခဏ ထည့် သွင်းပြောဆိုသင့်ကြောင်း ဂျာမန်သုတေသီ လမ်းမားစ်က အကြံပြုသည်။

“ကျနော်တို့စစ်တမ်းက မီဒီယာအနေနဲ့၊ အစိုးရအနေနဲ့ ဒီကပ်ရောဂါအကြောင်း လူထုကိုတင်ပြတဲ့အခါ ဘယ်လိုတင်ပြသင့်သလဲဆိုတဲ့အကြောင်း ပြောထားပါတယ်။ ပြီးခဲ့တဲ့ ရက်သတ္တပတ်အတွင်း ကူးစက်ခံခဲ့ရတဲ့ လူနာဦးရေနဲ့ ရောဂါတိုးနှုန်းကို ဖော်ပြ ရုံတင်မကဘဲ ဒီရောဂါတိုးနှုန်းအတိုင်းသာ  ဆက်ချီတက်နေခဲ့ရင် နောက်သုံးလေးရက် မှာ၊ နောက်တပတ်မှာ၊ နောက်တလမှာ ဘာဖြစ်နိုင်တယ်ဆိုတာကိုပါ တပါတည်း ရှင်းပြရမှာ ဖြစ်ပါတယ်။”

ဒီ Exponential Growth Bias လို့ခေါ်တဲ့ အချိန်နှင့်အမျှ ရောဂါ အဆတိုးခြင်း သဘောကို မသိနားမလည်မှု(အမြင်ကန်းမှု)ကို ကျော်လွှားနိုင်ခဲ့ရင် ဘာဖြစ်မလဲ။ လ အနည်းငယ်အတွင်း လူပေါင်း ငါးသန်းကျော် ရောဂါကူးစက်ခံခဲ့ရသည့် အမေရိကန် နိုင်ငံကို လမ်းမားစ်က ဥပမာပေးသည်။

“မတ်လကတည်းက ကျနော်တို့အနေနဲ့ ဒီအမြင်လွဲမှုကြီးကို ကျော်လွှားပြီး အမေရိကန်ပြည်သူတွေကို ဒီအမြင်လွဲမှုကြီးရဲ့ အ္တရာယ်ကို သဘောပေါက်အောင် လုပ်နိုင် ခဲ့ရင် ၉၉ ရာနှုန်းသော      အမေရိကန်ပြည်သူတွေဟာ ရောဂါကာကွယ်ရေးလုပ်ငန်းတွေကိုရင်ထဲအသည်းထဲကနေလက်ခံခဲ့လိမ့်မယ်လို့ကျနော်ယုံကြည်တယ်” ဟုသူကဆိုသည်။

ကပ်ရောဂါတခု ဖြစ်ပွားသည့်အခါ ကပ်ရောဂါကို မီးထိုးပေးသော အကြောင်း အချက်များစွာ ရှိပါသည်။ ဒီအကြောင်းအချက်တွေထဲ Exponential Growth Bias ဆိုတာ တခုအပါအဝင်ဖြစ်ကြောင်း စာရှုသူတို့အား လက်တို့လိုက်ရပါကြောင်း။

 

စာညွှန်း

Exponential growth bias: The numerical error behind Covid-19 by David Robson

https://www.bbc.com/future/article/20200812-exponential-growth-bias-thenumerical-error-behind-covid-19